初見マイクラ実況の裏でやっている、レッドストーンでの電卓作成。
それに必要なものをまとめていくサブシリーズだ。
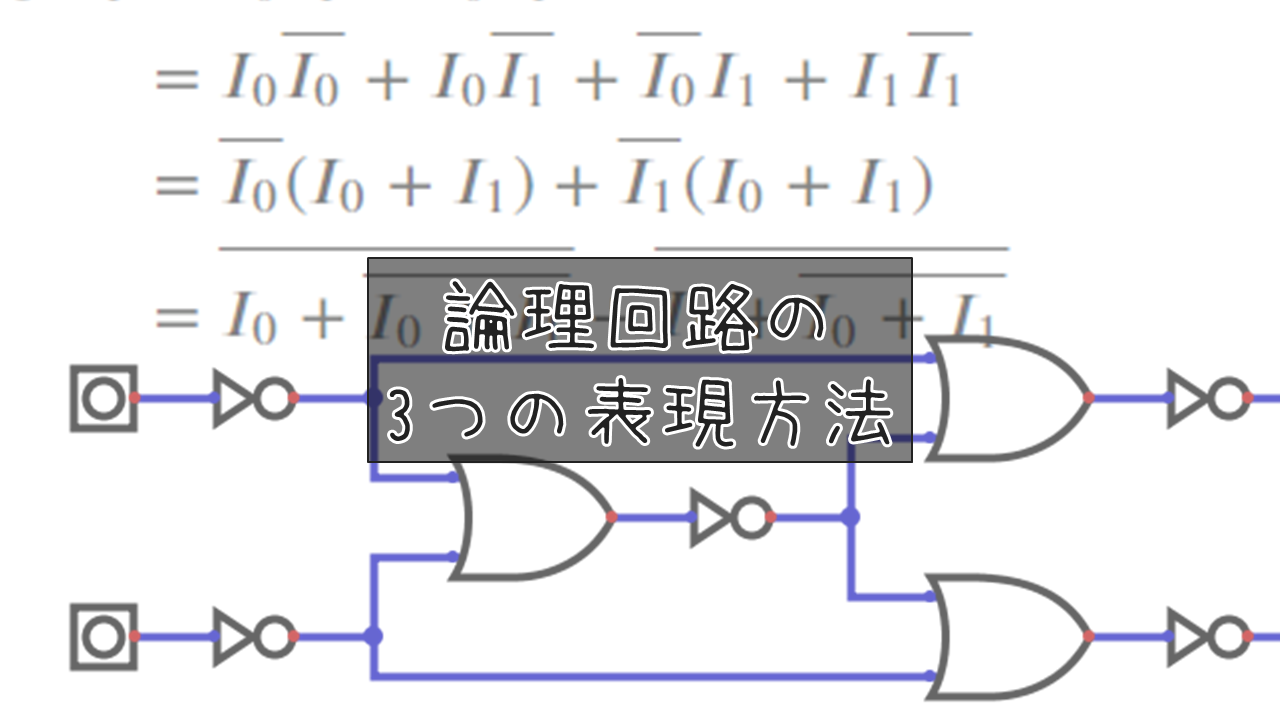
前回で論理回路が何か大雑把に分かったので、今回はそれをどう表現していくかに焦点を当てて確認していこう。
具体的には以下の3つだ。
- 真理値表
- 論理式(ブール代数)
- 論理回路図
あ、講座風な書き方をしているが、実体は私のメモなので、あまり気にしないで欲しい。
他の人に解説するつもりでまとめるのが私流の勉強方法なのだ。
論理回路の表現方法
さて、論理回路を組もうと言っても、いきなりレッドストーンを配置し始めるわけにもいかない。
まずは、どういう動きをさせるために、どのように組むかを考える必要がある。
つまり、なんらかの方法で論理回路を表現する必要がありそうだ。
というわけで、その表現方法を見ていこう。
真理値表
実はさらっと前回出してしまっていたもの。
真理値表とは、ある回路の入力の組み合わせ全てに対して、出力がどうなるべきかをまとめた表だ。
基本、何か論理回路…特に組合せ回路を作りたいとなった時に、真っ先に思い浮かぶものがこれ。
具体例は前回の各素子の表を見てもらえればと思う。
ちなみにだが、ただやりたいことを実現するだけなら、この真理値表だけでも論理回路を組むことは可能だ。
例えば、以下の入出力の関係を作りたいとする。
| \(I_0\) | \(I_1\) | 欲しい出力 |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
この時、この正体を知っていれば\(I_0\)が0、または\(I_1\)が1の時に出力を1にすればいい、と分かる。
これは含意と呼ばれる関係だ。
しかし、それを知らない、あるいは気づかない場合は、まず\(I_0\)のNOTと\(I_1\)のNOTをANDで結ぶ。
次に\(I_0\)のNOTと\(I_1\)をANDで結び、\(I_0\)と\(I_1\)もAND。
この3つのANDの結果をORで取る、ということになってしまう。
レッドストーンで組むと、最小の形と比べてなかなかの大きさになることが想像に難しくないだろう。
ようは、ゴリゴリ組むことでもやりたいことは一応実現可能なのだが…さすがにこれだけでは作業量だったり必要な資材量が必要以上に膨れ上がってしまう。
そのため、どうにか簡単にする必要があるのだが…その方法の一つが、次に紹介する論理式になる。
論理式(ブール代数)
というわけで、二つ目は論理式。
イメージとしては、一つ目の真理値表で確定させた入出力の関係を式に変換して、その式自体も法則によって書き換えて組むべき回路の中身を整理していく感じだ。
かなり量が多くなりそうだが…今後かなり重要になってくる部分でもあるので、しっかり見ていこう。
まず、入力をそれぞれ変数で表す。
これまでも使ってしまっていたが…よくInputの略で\(I\)という記号を使うので、今回もそれを使うことにしよう。
また、複数の入力がある場合、\(I_0\)、\(I_1\)、\(I_2\)、…といった形で、添え字をつけることが多い。
これと、後程紹介する素子に対応した演算記号で式を作り、その式全体の結果を出力とする、という書き方になる。
素子に対応した演算記号
前回紹介した6つの基本素子なのだが、そのうち4つには論理式側の記号も用意されている。
2つの入力を\(I_0\)、\(I_1\)として、その記号を紹介していこう。
まずOR素子、これは2つの入力あるいは別の式をプラス記号で結ぶ。
$$I_0 + I_1$$
このプラスは省略不可だ。
次にAND素子、2つの入力あるいは別の式をそのまま繋げて書くか、中点を挟んで書く。
$$\begin{eqnarray}
I_0 I_1 \\
I_0 \cdot I_1
\end{eqnarray}$$
ANDが省略可なので、他の記号は省略不可になっている、と覚えるといいだろう。
そしてXOR素子、これはORのプラスをさらに丸で囲んだ記号を使う。
$$I_0 \oplus I_1$$
最後にNOT素子、これは一つの入力だったので記号も一つの変数あるいは式に対しての記号だ。
そのNOTにする変数や式の上に横棒を伸ばす。
$$\overline{I_0}$$
演算記号は以上で、他にも通常の計算式と同じくカッコが使える。
その場合、カッコの中身を先に計算することになるので覚えておこう。
なお、計算の優先順位は、高い方からカッコ内、NOT内、AND、OR、XORとなっている。
ちなみに、NORとNANDは専用の演算記号が用意されていないが、OR、AND全体をNOTにすることで表現可能だ。
$$\begin{eqnarray}
\mbox{NOR : } \overline{I_0 + I_1} \\
\mbox{NAND : } \overline{I_0 I_1}
\end{eqnarray}$$
性質
ここまでの内容だけでは、単に式への書き換えしかできない。
が、この性質を利用することで論理式の真価が発揮される。
そりゃそうだろ、という内容も多いと思うが…念のため、簡単なものから提示していこう。
まず、一つの入力\(I\)に関する性質から。
- \(I + 0 = I\)
- \(I + 1 = 1\)
- \(I \cdot 0 = 0\)
- \(I \cdot 1 = I\)
- \(I + \overline{I} = 1\)
- \(I \cdot \overline{I} = 0\)
- \(I + I = I \cdot I = I\)
- \(\overline{\overline{I}} = I\)
最後の二重否定以外は、前回出した真理値表の部分を見てもらえればこの通りになっていることが分かると思う。
二重否定は、2回0と1を入れ替えるので、結局元に戻る、というだけだ。
次に、交換法則と呼ばれるもの。
NOTを除く5つの素子は、入力の前後を入れ替えても結果が変わらない。
$$\begin{eqnarray}
I_0 + I_1 & = & I_1 + I_0 \\
I_0 \cdot I_1 & = & I_1 \cdot I_0 \\
\overline{I_0 + I_1} & = & \overline{I_1 + I_0} \\
\overline{I_0 \cdot I_1} & = & \overline{I_1 \cdot I_0} \\
I_0 \oplus I_1 & = & I_1 \oplus I_0
\end{eqnarray}$$
そして、通常の計算でも使う分配法則。
よく使うのはORとANDのものなので、それを紹介しよう。
入力が3つに増え、以下のような関係が成り立つ。
$$\begin{eqnarray}
I_0 \cdot (I_1 + I_2) & = & I_0 \cdot I_1 + I_0 \cdot I_2 \\
I_0 + (I_1 \cdot I_2) & = & (I_0 + I_1) \cdot (I_0 + I_2)
\end{eqnarray}$$
上は普通の計算と同じだが、下がちょっと変わっているのでそこは注意ポイントだ。
さらに、結合法則。
ORとANDに関して、以下が成り立つ。
$$\begin{eqnarray}
(I_0 + I_1) + I_2 & = & I_0 + (I_1 + I_2) \\
(I_0 \cdot I_1) \cdot I_2 & = & I_0 \cdot (I_1 \cdot I_2)
\end{eqnarray}$$
ようは、同じ演算で三つ繋がっている時は、前から計算しても後ろから計算しても変わらないよ、ということ。
ここで注意なのだが、NORとNANDは結合法則が成り立たない。
その理由は後程解説するとして…最後の法則、ド・モルガンの定理。
$$\begin{eqnarray}
\overline{I_0 + I_1} & = & \overline{I_0} \cdot \overline{I_1} \\
\overline{I_0 \cdot I_1} & = & \overline{I_0} + \overline{I_1}
\end{eqnarray}$$
これは証明もできるが…それぞれ真理値表を書けば終わりなので、省略させてもらおう。
ちなみに、前回のNANDからANDを作ったのは、この二つ目の式を両方NOTにしたものを使っている。
$$I_0 \cdot I_1 = \overline{\overline{I_0 \cdot I_1}} = \overline{\overline{I_0} + \overline{I_1}}$$
では、これを使ってNORとNANDの結合法則が成り立たないことを証明してみよう。
まずはNORから。
$$\begin{eqnarray}
\overline{\overline{I_0 + I_1} + I_2} & = & (I_0 + I_1) \cdot \overline{I_2} \\
\overline{I_0 + \overline{I_1 + I_2}} & = & \overline{I_0} \cdot (I_1 + I_2)
\end{eqnarray}$$
これで、\(I_0 = 1\)、\(I_1 = 0\)、\(I_2 = 0\)だったとすると、上の式は1、下の式は0になるので成り立たないことが分かると思う。
次にNAND、そろそろ中点を省略して書いてしまおう。
$$\begin{eqnarray}
\overline{\overline{I_0I_1}I_2} & = & I_0I_1 + \overline{I_2} \\
\overline{I_0 \overline{I_1I_2}} & = & \overline{I_0} + I_1I_2
\end{eqnarray}$$
これも上と同じく\(I_0 = 1\)、\(I_1 = 0\)、\(I_2 = 0\)で上の式が1、下の式が0となる。
結合法則を使う場合には十分注意しておこう。
XORの変形の意味
これで、前回や本編で出したXORの変形を説明できるようになった。
式を以下に再掲しよう。
$$\begin{eqnarray}
I_0 \oplus I_1 & = & I_0 \overline{I_1} + \overline{I_0} I_1 \\
& = & I_0 \overline{I_0} + I_0 \overline{I_1} + \overline{I_0} I_1 + I_1 \overline{I_1} \\
& = & \overline{I_0} (I_0 + I_1) + \overline{I_1} (I_0 + I_1) \\
& = & \overline{I_0 + \overline{I_0 + I_1}} + \overline{I_1 + \overline{I_0 + I_1}}
\end{eqnarray}$$
方針は前回書いた通り、比較的小さいOR、NOTの素子のみを用いて表現することだった。
一つ目は、単にXORの定義通りに書き換えたのみ。
両方異なっている場合にのみ1を具体的に書き表しただけだ。
次の変形は、同時に二つのことを、さらに2か所で行っている。
まず、ある値と0とのORは変化しないので、0をORで繋げる。
その0について、ある値と同じ値の否定をANDで取ると0になるので、それで置き換えている。
今回は、\(I_1 \overline{I_1}\)、\(I_2 \overline{I_2}\)の二つだ。
そして、次では分配法則を逆向きに使っている。
もちろんだが双方向への変換が可能だ。
最後はド・モルガンの定理による変形だ。
これで、(結果的にNORも出てきているが…)ORとNOTだけでXORを表現できた、というわけだ。
ちなみに、もうちょっと簡略化できたという形の式は以下の通り。
$$\begin{eqnarray}
I_0 \oplus I_1 & = & (I_0 + I_1) \overline{I_0 I_1} \\
& = & I_0 \overline{I_0I_1} + I_1 \overline{I_0I_1} \\
& = & \overline{\overline{I_0} + I_0I_1} + \overline{\overline{I_1} + I_0I_1}\\
& = & \overline{\overline{I_0} + \overline{\overline{I_0} + \overline{I_1}}} + \overline{\overline{I_1} + \overline{\overline{I_0} + \overline{I_1}}}
\end{eqnarray}$$
出発点は前回書いた通り、ORとNANDのAND。
まずは分配法則でORの方をバラバラにする。
そこから両方に対してド・モルガンの定理で変形し、その中のAND部分をもう一回ド・モルガンの定理で変形。
…と書いてきたが、実際は適当にレッドストーンを配置してたらこうなった、というのが正直なところだったりする。
論理回路図
最後の表現方法、論理回路図を見てみよう。
これは、図で直接回路を記述する表現方法だ。
これを書くくらいならレッドストーン回路を直接作ればいいのでは?と思うかもしれないが…それだと規模が大きくなってきた時に全体像が把握しづらいだろう。
それに、一回組んだものが間違っていた時に修正がかなり面倒になってしまう。
そのため、基本は論理回路図で組む回路を表現し、それを使ってレッドストーン回路でも組んだものを紹介する、という形で進めようと思う。
今回は、フリーのシミュレータであるDigitalを使わせてもらうため、記号などもそれで説明しよう。
まず、各基本素子に専用の記号が用意されている。
その一覧は以下の通り。
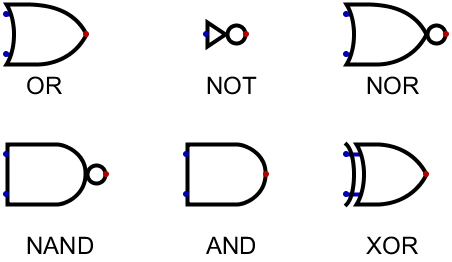
この図の青点が入力、赤点が出力となっている。
ここに線を引いていくことで、回路を表現していくのだ。
次に入出力、入力はしばらくボタンを使わないので、レバーの代用を出しておこう。

これで回路を組んでいく。
幾つか例も出してみよう。
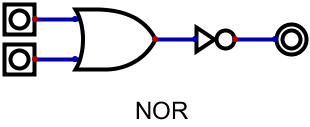
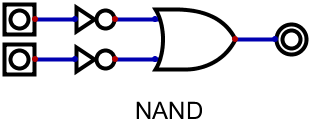
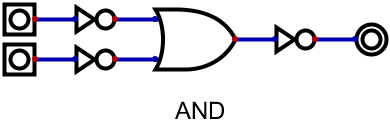
まず、前回やったレッドストーン回路の形で、NOR、NAND、ANDを書いてみると以下の通り。
また、縮小前・縮小後のXOR回路は以下の通りだ。
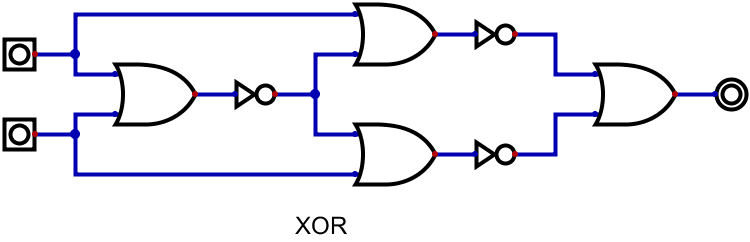
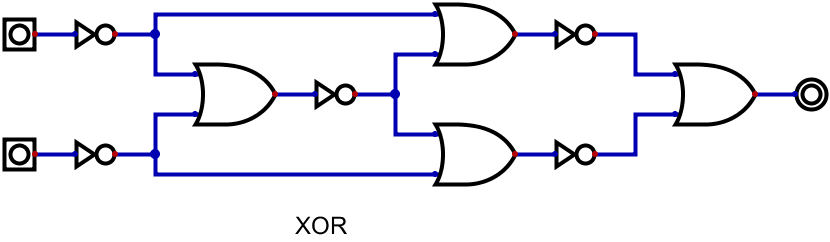
…これだけ見ると、レッドストーンでは縮小できていても、論理回路図では逆に大きく見えてしまう。
大きく見えるというか、NOTが二つ増えているので実際に大きくなっている。
つまり、レッドストーン回路の場所的なリソースは、これだけでは測れない。
レッドストーン回路専用のシミュレータを探すことも一瞬考えたのだが…やはりネタバレが怖いので、今回はこれで進めさせてもらおう。
ちなみに、XOR回路で線が交わっているところに点が打たれている部分があると思う。
これは、そこで分岐することを意味している。
今後、点がない線の交差も出てくると思うが、その時は表記上交差してしまっているだけなので、そこは気を付けよう。
おわりに
今回は論理回路をどう表現するの?という話だったので、あまり内容には入れなかった。
が、これを使って設計し、実際にレッドストーンで組み上げていくことになるので、やはり理解しておきたいところだろう。
私も、今後進めてて分からなくなったらここに戻ってくることにしよう。
さて、次からいよいよ電卓への第一歩だ。
…が、論理回路からも少し離れた話になるだろう。
論理回路で計算をする上で欠かせない、2進数という考え方を見ていく。
四則演算の基礎になるので、しっかり勉強していきたい。
2022/6/9 次回記事更新
オマケ:レッドストーン回路の遅延
一応カテゴリー的にはレッドストーン回路の攻略なので、本編と関係無いが…さすがに一つくらいは触れておこう。
前回の基本素子の時に気づいているのだが、何かしらの条件でレッドストーン回路には遅延が発生する。
まだ厳密には試していないが…恐らく、レッドストーントーチ使用時にわずかな遅延が発生する。
基本素子のうち、XOR回路だけ違和感があるくらいには結果が出るまで時間がかかっているのだ。
他にも、リピーターでも遅延が発生し、こちらは4段階に遅延時間を調節できることが分かっている。
このあたりまでは分かっているが、まだ具体的にどこでどの程度の遅延があるかは分かっていない。
今後組む電卓はかなり大規模で、この遅延時間もかなりのものになるだろう。
そこで、通常の論理回路の設計に加え、遅延時間をどうやったら最小にできるかや、待つ必要がある部分も考える必要が出てくると思う。
シリーズで作るつもりの部品についても、可能ならそこまで考えてみることにしよう。