初見マイクラ実況のPart7、Part10あたりで軽くではあるがレッドストーン回路について検証を行った。
それ以降は本編が終了してから、ということにしていたのだが…現在、ネザーも多少攻略が進んでおり、作成できるアイテムも増えてきた。
現段階で、一応本編中にも言った目標である電卓も作れそうだなと感じているところだ。
というわけで、今回から一旦電卓に必要な部品を作るためのあれこれを試し、その結果をまとめていこうと思う。
…正直、我慢できなかった。
さて、先に断っておくが、本編と同様にWiki等の外部情報は一切調べず、自力で検証を重ねていく。
そのため、誤り等含まれる可能性が十分にあるので、そこは注意してほしい。
また、こういう縛りでやりたいため、間違っている部分があっても気づくかなとニヤニヤしながら見てもらえれば幸いだ。
なお、この内容を動画にするかは未定だ。
最終的に電卓を作る時にはその様子、あるいは完成形くらいは動画にすると思う。
今回は初回ということで、本編でやった内容の復習メインで進めていこう。
具体的には論理回路自体の軽い紹介と、基本素子の作り方だ。
また、オマケで現状分かっているレッドストーン関係のアイテムも幾つか様子を見てみる。
そもそも論理回路って?
まず、論理回路自体の説明から。
論理回路とは、0と1の2択の入力を幾つか入れ、その結果としてこれまた0と1の2択を出力する回路のこと。
プログラマーなら馴染みがあると思うが、この0と1の2択のことを論理値などと呼ぶので、そこから論理回路という名前がついているのだろう。
これで何ができるかというと、まず本編でも出した、2か所にスイッチがある電気が簡単な例の一つ。
これは、どちらのスイッチを切り替えても、今電気がついていれば消え、消えていればつく、という動きをする。
回路としては、2つのスイッチの状態が同じなら消灯、異なるなら点灯という仕組みだ。
こんなものが、論理回路で作ることができる。
もっと言うと…今皆さんがお使いのPCやスマホ。
これも、(とんでもなく複雑だが…)この論理回路で作成可能だ。
とはいえ、そこまでやると年単位で時間がかかるので、妥協点として電卓を選んだ、というわけだ。
なお、レッドストーン攻略のため、一旦電卓としての設計は省くことにする。
が、必要な部品についてはその時に設計する様子もお見せすることにしよう。
また、同様に必要な考え方もまとめていく。
その時は、レッドストーン関係なく純粋な論理回路の説明になるのだが…まあ、興味があれば見てみて欲しい。
ちなみに、さすがに論理回路は情報縛りはせず、ガンガン調べさせてもらう。
サブシリーズの目標
本サブシリーズの目標は、メインの目標である電卓に必要な回路を作ることだ。
実際は、コメントで教えてもらったクリエイティブモードで電卓を作ろうと考えているが、いきなりやっても難しいだろう。
そこで、一旦電卓を構成する色々な回路を試しに作ってみよう、というのが本シリーズの立ち位置だ。
また、クリエイティブモードでは本編でまだ未入手のアイテムも使えてしまう。
そのネタバレ防止のためにも、本編と同じワールドで検証を進めていく。
ちなみに、具体的に作ろうとしている回路は…
- 組合せ回路
- 各基本素子
- 加算器
- エンコーダ
- デコーダ
- 四則演算器
- 順序回路
- フリップフロップ
- クロック
- レジスタ
あたりだろうか。
ざっと思いついたものを挙げただけなので、今後増える可能性も十分ある。
それぞれの詳細は、実際に作る時に解説しよう。
補足:組合せ回路と順序回路
具体的に組みたい回路の分類として、組合せ回路と順序回路という名前を出した。
この二つを少しだけ紹介しておこう。
まず、組合せ回路とは、その時の入力によってのみ、出力が一意に決定するような回路のことだ。
例えば、先ほど出した2か所にスイッチがある電気。
これは、純粋に2つの入力の状態だけから、電気がつくかどうかを求めることができるため、組合せ回路だ。
…これだけだと分かりづらいと思うので、順序回路も説明してみよう。
順序回路は、入力に加えて現在の出力も加味して、次の出力が決定するような回路のことだ。
例えば、ある入力が1になったら、現在の出力を反転させるといったことが可能になる。
そんな回路の場合、元々出力が0だったら1になるし、1だったら0になる。
つまり、同じ1の入力でも、出力が変わる場合があるのだ。
これを応用すると、一時的に0か1の情報を保持することができるようになる。
電卓では、一つ目の数字を入力して四則演算ボタンでそれを保持し、二つ目の数字と計算する必要があるため、この順序回路も必要になる。
この2つの違いは、進めていけばよりわかりやすくなると思うので、まだ分からなくても大丈夫だ。
しばらくは組合せ回路のみの話になるので、一旦順序回路のことを忘れてもらっても構わない。
使用するアイテム
では、現段階分かっている限りの使うアイテムを見ていこう。
まず、入力は大きく二つ、レバーとボタンを用いる。
ボタンは実際の電卓と同じような挙動をするため、構築時は全てボタン入力にするつもりだ。
ただし、一定時間で勝手に戻るのでは、検証には使いづらい。
そこで、検証時にはレバーも併せて使うことにする。
次に、信号を伝達するのはもちろんレッドストーンダスト。
回路を構成するためにレッドストーントーチ、この使い方は基本素子の中で見ていく。
その他、送信距離の延長や必要な時には方向の制御を行うため、リピーターも用いる。
出力には、つい最近見つけたグロウストーンからのクラフト、レッドストーンランプを用いることにしよう。
ちょうど探していたので、見つかってよかった。
一つ補足で、本編の動画に「どうやってレッドストーンで数字を表現するのか」といった趣旨のコメントを頂いたことがある。
それは、デコーダあたりの解説でお答えすることにしよう。
なお、論理回路の説明で0と1の2択と書いたが、レッドストーンダストが光っている状態を1、消えている状態を0とする。
今回使う出力のランプも1の時に点灯、0の時に消灯なので、直感的に考えやすい。
ちなみに、現時点で幾つか、上記以外で回路に関係あるアイテムが見つかっている。
具体的には二つ、コンパレーターとオブザーバーだ。
これらは現時点では電卓に使うか分からないが…本記事後半でどんなものかだけ見てみることにしよう。
論理回路の基本素子
早速、論理回路を組み始めてしまおう。
Part9あたりでも軽く触れたが、論理回路には3つ(+3つ、計6つ)の基本となる素子がある。
これがないと何もできないが、逆にこれがあれば電卓は組める…はず。
その素子たちを、論理回路の観点、レッドストーン回路の観点両方で見ていこう。
なお、紹介の順番はレッドストーン回路で作る順で見ていく。
レッドストーン回路では最初の2つだけ直接作ることができ、残りの4つは最初の2つを組み合わせて作ることになる。
OR素子
一つ目はOR素子と呼ばれるもの。
2つの入力と1つの出力を持ち、入力のいずれかでも1なら1を出力し、両方とも0なら0を出力する。
| 入力1 | 入力2 | OR出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
レッドストーン回路では、シンプルにレッドストーンダストを繋げるだけでこれが実現可能だ。
組み方と動作の様子は以下の動画を参照してほしい。
NOT素子
これは1つの入力と1つの出力を持つ素子で、入力の0と1を入れ替えたものが出力になる。
| 入力 | NOT出力 |
|---|---|
| 0 | 1 |
| 1 | 0 |
よく、~の否定とか~のNOTとかといった言い方をするが、それも0と1を入れ替えることを意味している。
今後もよく使うことになるので、覚えておくといいだろう。
レッドストーン回路では、レッドストーントーチを使用する。
これは、通常は常に1の信号を出力するアイテムなのだが、これが設置されたブロックに1の信号が入力されると、今度は0を出力するようになる。
この動きがNOTそのものなので、そのまま使えばOKだ。
組み方と動作は以下の動画だ。
NOR素子
ここからは組み合わせていくことになる。
NOR素子は、ORの結果を否定にしたもの…つまり、ORの後ろにNOTを入れたものになる。
先頭のNが、NOTの意味になる。
言葉で言えば、2入力とも0の時に限り1を出力し、それ以外(入力の片方でも1)は0を出力する。
| 入力1 | 入力2 | NOR出力 | (参考)OR出力 |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 |
回路の組み方もそのままで、レッドストーンダストをそのまま繋げ、その後ろにNOTを組めば完成だ。
組み方と動作の動画は以下。
NAND素子
ここで、順番がややこしくなる。
通常の論理回路では、先に後述するAND素子の紹介があり、それとNOTを使ってNAND素子を説明する。
が、レッドストーンでは先にこのNAND素子を作って、その結果を否定することでAND素子を作ることになる。
これは、ORとNOTが先に作れていることが原因なのだが…いや、そこを深掘りするのはやめよう。
NAND素子は、入力のいずれか片方でも0なら1を出力し、両方1の時に限り0を出力する素子だ。
言い換えると、両方とも1の時にのみ1を出力するAND素子の否定、ということになる。
| 入力1 | 入力2 | NAND出力 |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
レッドストーンの組み方も少し大きくなってくる。
まず、2つの入力を両方ともNOTにする。
その結果をORで取ればNANDの完成になる、といった感じだ。
実際に組んだ様子と動作は以下の通り。
AND素子
もう上に書いてしまったが、AND素子は2入力1出力で、入力が両方とも1の時に限り1を出力する素子だ。
通常の論理回路では、真っ先に紹介されるものだったりする。
| 入力1 | 入力2 | AND出力 | (参考)NAND出力 |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
組み方も先ほど上に書いた通りで、NAND素子を作り、その後ろにNOT素子をくっつけてあげれば完成だ。
実際の様子は以下の通り。
さて、ここまでは恐らく出したものが最小の回路になっていると思う。
しかし、次がなかなかに厄介だ。
XOR素子
XOR素子は、日本語だと排他的論理和と言って、ちょっと特殊な動き方をする。
2入力1出力で、入力の0と1が一致していれば0を、異なっていれば1を出力する、という動作だ。
| 入力1 | 入力2 | XOR出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
先ほどから何回か例に出している2か所スイッチの電気がまさにこれだ。
レッドストーンにおける組み方がなかなかに厄介で、シンプルに考えるとORの結果とNANDの結果をANDで取れば作成は可能。
| 入力1 | 入力2 | 入力1 OR 入力2 | 入力1 NAND 入力2 | XOR出力(左二つのAND) |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
しかし、これをそのままレッドストーンで組もうとすると、なかなかに回路が大きくなってしまう。
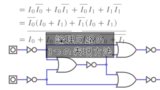
そこで、色々と式をこねくり回して、なんとか小さくできないかと考えたのが、動画でも出した以下の式だ。
$$\begin{eqnarray}
I_0 \oplus I_1 & = & I_0 \overline{I_1} + \overline{I_0} I_1 \\
& = & I_0 \overline{I_0} + I_0 \overline{I_1} + \overline{I_0} I_1 + I_1 \overline{I_1} \\
& = & \overline{I_0} (I_0 + I_1) + \overline{I_1} (I_0 + I_1) \\
& = & \overline{I_0 + \overline{I_0 + I_1}} + \overline{I_1 + \overline{I_0 + I_1}}
\end{eqnarray}$$
何をしているかというと、ORとNOTだけで式を表現している。
この変形の詳細は次回解説するが…ようはORとNOTが直接作れて小さく、そこまで要素を分解することで、より小さくできないかと試していたのだ。
これで組んだものと動作の様子は以下の動画だ。
…ちなみに、この動画を撮影した時に色々いじくり回したら、なんか小さくできたっぽい。
これが最小かどうかもまだ分からないが…一旦、以下の形に落ち着いた。
これを数式で表現すると以下の通り。
$$\begin{eqnarray}
I_0 \oplus I_1 & = & (I_0 + I_1) \overline{I_0 I_1} \\
& = & I_0 \overline{I_0I_1} + I_1 \overline{I_0I_1} \\
& = & \overline{\overline{I_0} + I_0I_1} + \overline{\overline{I_1} + I_0I_1}\\
& = & \overline{\overline{I_0} + \overline{\overline{I_0} + \overline{I_1}}} + \overline{\overline{I_1} + \overline{\overline{I_0} + \overline{I_1}}}
\end{eqnarray}$$
先ほどちらっと「ORとNANDのANDを取れば」みたいなことを書いたが、そこから出発することでこの形に持ってこれた。
今後も、より小さくする方法がないか探してみることにしよう。
見つけたアイテムたちの検証
さて、今回最後になるが、上で出した二つのアイテム、コンパレーターとオブザーバーについて動作を確認していこう。
オブザーバー
先に簡単そうなオブザーバーから。
日本語にすると監視器という感じで、試した限りはその名の通り、アイテムの状態を監視できるアイテムのようだ。
前に置かれたアイテムの状態が変わる(設置される、壊されるなど)と、一瞬だけ1の信号を送り出すことができる。
もちろん前にレッドストーンダストがあれば、その0と1が切り替わったタイミングも検知してくれる。
今のところ、こいつはクロックという回路に使えそうかなぁと思っている。
厳密には、これでクロック自体を作るのではなく、クロックの代わりにできないか、といった感じだ。
コンパレーター
コンパレーターを日本語にすると比較器で、まあその名の通り2つの信号の強さを比較できる。
上にちらっと書いた通り、レッドストーンダストには信号の送信限界距離があり、検証した結果は15ブロック分だった。
で、信号源から離れると赤色も弱まっており、内部的に信号の強さが数値として存在しているらしい。
コンパレーターでは、二つの信号を特定の方向から入力することで、その強さの違いにより出力が変わる。
例えば、背面へ強さ10の信号を、側面へ強さ7の信号を入力すると、背面の方が大きいので強さ10の信号が出力される。
同じ強さでも出力は行われ、背面の方が弱くなると出力が0になる。
また、コンパレーターはモードの変更ができるようで、変えると強度の減算ができるようになる。
先ほどの例と同じく背面へ強さ10の信号、側面へ強さ7の信号を入力すると、差分の強さ3で信号が出力される。
…これについては、ぶっちゃけ使い道がよく分かっていない。
まあ、今回の論理回路には恐らく使わないだろう…
おわりに
初回ということで、基本は本編でやった検証の復習を進めてみた。
まだ検証が甘い部分もあるが…あまりそこに手をかけていても先に進まないので、一旦これで良しとさせてもらおう。
もし何か分かれば、該当箇所に追記するか、どこかのオマケで触れることにしよう。
次回からは…いきなりだが数回分レッドストーンから離れ、論理回路のお話を書いていく。
この話が電卓に絡んでくるので、メモを残させてもらいたい、という意図だ。
具体的には、次回は論理回路の表現方法を幾つか紹介し、次々回は計算を考える上で避けては通れない2進数を扱っていこう。
それを踏まえ、その次に加算器という回路をレッドストーンで作る、という流れを想定している。
かなり数学チックな話になるが、見てもらえれば幸いだ。
2022/6/8 次回記事更新